PASAR ESTE CUADRO A SU CUADERNO DE APUNTES
miércoles, 12 de octubre de 2011
lunes, 10 de octubre de 2011
TALLER GEOMETRÍA
Amigo estudiante a continuación encuentra un taller para resolver:
INSTITUCIÓN EDUCATIVA COLEGIO NUESTRA SEÑORA DE BELÉN
TALLER: ÁNGULOS
Alumno: Grado: 6 “A - B - C”
Asignatura: Matemáticas Periodo: IV
Docente: Manuel Enrique Rivera / Darly K. Guerrero. Fecha: 10/10/11
1. Con la ayuda del transportador halla el valor de los siguientes ángulos:

b) Cuál es el ángulo que forman las manecillas del reloj: a) a las 6:00, b) a las 2:30 y c) a las 9:30. (Dibuja el ángulo respectivo en cada reloj y escribe en la línea el valor y tipo del ángulo que se forma)

3. Indica, según la posición, el tipo de ángulos
INSTITUCIÓN EDUCATIVA COLEGIO NUESTRA SEÑORA DE BELÉN
TALLER: ÁNGULOS
Alumno: Grado: 6 “A - B - C”
Asignatura: Matemáticas Periodo: IV
Docente: Manuel Enrique Rivera / Darly K. Guerrero. Fecha: 10/10/11
1. Con la ayuda del transportador halla el valor de los siguientes ángulos:

2. Observa el grafico y responde:
a) ¿Qué ángulo forman las mancillas de cada reloj?
b) Cuál es el ángulo que forman las manecillas del reloj: a) a las 6:00, b) a las 2:30 y c) a las 9:30. (Dibuja el ángulo respectivo en cada reloj y escribe en la línea el valor y tipo del ángulo que se forma)

5. Completa la siguiente tabla:
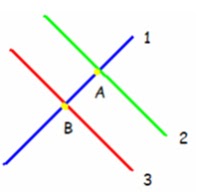
6. Observa el grafico y responde:
• Las rectas 1 y 2 son: ____________
• Las rectas 2 y 3 son: ____________
• Las rectas 1 y 3 son: ____________
• El punto donde se cortan las rectas 1 y 2 es: ________
• El punto donde se cortan las rectas 1 y 3 es: ________
7) Completa:
• Dos rectas ___________________ Forman cuatro ángulos rectos.
• Dos rectas ____________________ Se cortan en un punto
• Un ángulo _________________ es mayor que un ángulo recto.
• Un ángulo _________________ es menor que un ángulo recto.
miércoles, 29 de junio de 2011
EVALUACIÓN TIPO ICFES PERIODO II
COL. NTRA. SRA. DE BELÉN - MATEMÁTICAS – EVAL. TIPO ICFES GRADOS SEXTOS – PERIODO II
En un almacén de ropa de Cúcuta los precios fluctúan de acuerdo a la calidad de los artículos, en múltiplos de $10.000, así las camisas van desde $30.000 hasta $120.000; los pantalones desde $80.000 hasta $140.000; los zapatos desde $100.000 hasta $250.000 y las correas desde $10.000 hasta $100.000 y el bolívar (Bs) lo reciben a $0,50.
1) La cantidad mínima para comprar tres artículos diferentes es:
A) $30.000 B) $210.000 C) Menos de $600.000 D) $120.000
2) Comprar un estreno completo pagando en bolívares, cuesta mínimo:
A) Bs 440.000 B) Bs 1.220.000 C) Bs 305.000 D) Entre 305.000 y 1.300.000 Bs.
3) Para comprar dos estrenos completos de la mejor calidad se debe pagar:
A) $440.000 B) $1220.000 C) $305.000 D) Màs de $400.000
4) Un caballero tiene $950.000 decide llevar un par de zapatos y una correa de la mejor calidad y el resto del dinero entre pantalones y camisas, pero que sean dos camisas por cada pantalón y de la mejor calidad posible juntos, la mejor opción es:
A) 1 pantalón y 2 camisas. B) 2 pantalones y 4 camisas.
C) 3 pantalones y 6camisas D) 4 pantalones y 8 camisas
5) No importando la calidad de las prendas, pero llevando el mismo número de cada una de ellas, con $300.000 y Bs 300.000, la cantidad de combos posibles es:
A) 3 combos B) Menos de 4 combos C) 4 combos D) 2 combos
El papá de Pedrito estudiante de 6° grado del colegio Nuestra Sra. De Belén le dice: tengo tres trozos de palo de escoba de 30 cms., 45 cms. y 90 cms. Como usted ya tiene suficientes conocimientos de matemáticas, necesito que me colabore con las siguientes preguntas:
6) ¿Cuál es el tamaño más grande que pueden tener los pedazos, en que corte los palos de escoba, para que se desperdicie la menor cantidad posible de madera?
A) 10 cms. B) 15 cms. C) 20 cms. D) 30 cms.
7) ¿Cuántos cortes debo hacer para obtener estos pedazos?
A) 8 cortes B) 11 cortes C) 3 cortes D) 9 cortes
Luís, Jorge y Daniel fueron a practicar sus deportes al autodromo: Luís en bicicleta de carreras, Jorge en bicicleta montañera y Daniel en moto. Si Daniel demora 20 minutos en darle la vuelta al circuito, Luís 30 minutos y Jorge 40 minutos y los tres parten a las 9:30 a. m. del mismo punto de salida.
8) ¿A qué hora volverán a pasar los tres a la vez por el mismo punto de salida?
A) 60 minutos después B) 120 minutos después C) A las 10:30 a. m. D) A las 11:30 a. m.
9) En este momento que vuelven a pasar los tres a la vez por el punto de salida ¿Cuántas vueltas han dado Daniel, Luís y Jorge respectivamente?
A) 3, 4 y 6 vueltas B) 4, 3 y 6 vueltas C) 6, 4 y 3 vueltas D) 4, 6 y 8 vueltas
El Profesor Enrique para comprobar si sus estudiantes entendieron los conceptos de potenciación, radicación y logaritmación, hace a sus discípulos algunas preguntas como esta:
10) De las siguientes expresiones ¿cuál representa un cuadrado?
En un almacén de ropa de Cúcuta los precios fluctúan de acuerdo a la calidad de los artículos, en múltiplos de $10.000, así las camisas van desde $30.000 hasta $120.000; los pantalones desde $80.000 hasta $140.000; los zapatos desde $100.000 hasta $250.000 y las correas desde $10.000 hasta $100.000 y el bolívar (Bs) lo reciben a $0,50.
1) La cantidad mínima para comprar tres artículos diferentes es:
A) $30.000 B) $210.000 C) Menos de $600.000 D) $120.000
2) Comprar un estreno completo pagando en bolívares, cuesta mínimo:
A) Bs 440.000 B) Bs 1.220.000 C) Bs 305.000 D) Entre 305.000 y 1.300.000 Bs.
3) Para comprar dos estrenos completos de la mejor calidad se debe pagar:
A) $440.000 B) $1220.000 C) $305.000 D) Màs de $400.000
4) Un caballero tiene $950.000 decide llevar un par de zapatos y una correa de la mejor calidad y el resto del dinero entre pantalones y camisas, pero que sean dos camisas por cada pantalón y de la mejor calidad posible juntos, la mejor opción es:
A) 1 pantalón y 2 camisas. B) 2 pantalones y 4 camisas.
C) 3 pantalones y 6camisas D) 4 pantalones y 8 camisas
5) No importando la calidad de las prendas, pero llevando el mismo número de cada una de ellas, con $300.000 y Bs 300.000, la cantidad de combos posibles es:
A) 3 combos B) Menos de 4 combos C) 4 combos D) 2 combos
El papá de Pedrito estudiante de 6° grado del colegio Nuestra Sra. De Belén le dice: tengo tres trozos de palo de escoba de 30 cms., 45 cms. y 90 cms. Como usted ya tiene suficientes conocimientos de matemáticas, necesito que me colabore con las siguientes preguntas:
6) ¿Cuál es el tamaño más grande que pueden tener los pedazos, en que corte los palos de escoba, para que se desperdicie la menor cantidad posible de madera?
A) 10 cms. B) 15 cms. C) 20 cms. D) 30 cms.
7) ¿Cuántos cortes debo hacer para obtener estos pedazos?
A) 8 cortes B) 11 cortes C) 3 cortes D) 9 cortes
Luís, Jorge y Daniel fueron a practicar sus deportes al autodromo: Luís en bicicleta de carreras, Jorge en bicicleta montañera y Daniel en moto. Si Daniel demora 20 minutos en darle la vuelta al circuito, Luís 30 minutos y Jorge 40 minutos y los tres parten a las 9:30 a. m. del mismo punto de salida.
8) ¿A qué hora volverán a pasar los tres a la vez por el mismo punto de salida?
A) 60 minutos después B) 120 minutos después C) A las 10:30 a. m. D) A las 11:30 a. m.
9) En este momento que vuelven a pasar los tres a la vez por el punto de salida ¿Cuántas vueltas han dado Daniel, Luís y Jorge respectivamente?
A) 3, 4 y 6 vueltas B) 4, 3 y 6 vueltas C) 6, 4 y 3 vueltas D) 4, 6 y 8 vueltas
El Profesor Enrique para comprobar si sus estudiantes entendieron los conceptos de potenciación, radicación y logaritmación, hace a sus discípulos algunas preguntas como esta:
10) De las siguientes expresiones ¿cuál representa un cuadrado?
sábado, 11 de junio de 2011
jueves, 9 de junio de 2011
RELACIONES ENTRE POTENCIACIÓN - RADICACIÓN Y LOGARITMACIÓN
JOVENES ESTUDIANTES CON BASE EN ESTE EJERCICIO ELABORE UNA TABLA Y DELE 2 VALORES CONOCIDOS PRIMERO DE POTENCIACIÓN Y HALLE LOS DEMAS DESPUES 2 DE LA RADICACIÓN HAGA LO MISMO Y POR ÚLTIMO 2 DE LA LOGARITMACIÓN Y HALLE LOS DEMÁS. BUENA SUERTE.
martes, 7 de junio de 2011
lunes, 6 de junio de 2011
MÁXIMO COMÚN DIVISOR
El máximo común divisor de dos ó más números es el más grande de los divisores que es común de los dos.
Miremos los números 12, 18 y 24. Saquemos los divisores de estos números.
Divisores:
12 = (1, 2, 3, 4, 6. 12) 18 = (1, 2, 3, 6, 9, 18) 24 = (1, 2, 3, 4, 6, 8, 12, 24)
Señalemos los divisores comunes y escojamos el mayor de ellos.
12 = (1, 2, 3, 4, 6. 12) 18 = (1, 2, 3, 6, 9, 18) 24 = (1, 2, 3, 4, 6, 8, 12, 24)
* * * * * * * * * * * * *
El mayor de los divisores comunes es 6, este es el máximo común divisor de 12, 18 y 24.
Hay una forma más fácil y práctica de hallar el máximo común divisor y es mediante la descomposición de factores:
Trabajo en clase:
Hallar el M. C. D. de: a) 18, 24 y 30 b) 20, 40 y 60 c) 18, 27 y 81
Problemas de aplicación del Máximo Común Divisor:
El máximo común divisor se puede aplicar en la solución de problemas que involucran repartición de cantidades, como la longitud.
Se desea cortar 3 varillas en partes iguales de tal forma que no sobre ningún pedazo. ¿Cuál será la longitud más grande que puede tener cada trozo y cuantos pedazos se obtienen si las varillas miden 30, 42 y 54 cm ?
Tabla de datos:
L1 = 30 cm .
L2 = 42 cm .
L3 = 54 cm .
¿Cuántos trozos iguales se obtienen?
¿Cuántos?
Este problema pertenece a M. C. D. de números naturales.
Planteamos la ecuación ó ecuaciones respectivas:
Long. de cada pedazo = M. C. D. de L1, L2 y L3
No hay que hacer conversiones, pues todas las longitudes están en centímetros.
Hacemos las conclusiones:
La longitud de cada pedazo es de 6 cm . que fue el resultado de hallar el M.C.D. de las longitudes de las tres varillas de 30 cm ., 42 cm . y 54 cm .
El número de pedazos es de 21 que fué el resultado de dividir la longitud de cada varilla de 30, 42 y 54 cms. entre el M. C. D. de 6 cm. y luego hacer la suma de estos cocientes 5 + 7 + 9.
viernes, 13 de mayo de 2011
PRODUCTO DE POLINOMIOS ARITMÉTICOS
Producto de un número natural por un polinomio aritmético.
Para multiplicar un número natural por un polinomio aritmético, se multiplica el número natural por cada uno de los términos del polinomio, teniendo en cuenta el signo que se antepone a cada uno de ellos.
Producto de dos polinomios.
Se procede de la misma manera que en los casos anteriores pero teniendo en cuenta que ya el primer factor es también un polinomio y se debe colocar el signo de cada factor y abrir un paréntesis, luego hacer las operaciones y eliminar los signos de agrupación utilizados. El paréntesis de la multiplicación del primer número por el polinomio se puede no colocar, como en el siguiente ejemplo, el correspondiente a las líneas continuas.
martes, 12 de abril de 2011
domingo, 27 de marzo de 2011
OPERACIONES ENTRE CONJUNTOS
Se pueden combinar los elementos de dos conjuntos para producir conjuntos nuevos mediante diferentes operaciones.
Unión entre conjuntos:
Dados dos conjuntos A y B, el conjunto formado por la reunión de los elementos de A con los elementos de B (sin repetir), es decir los elementos comunes y no comunes de ellos se llama unión de A y B
y se simboliza así: A È B = íx / x Î A Ú x Î Bý.
Ejemplo: Si A= í0, 2, 3, 4, 6, 8 ý B = í0, 2, 4, 8 ý C = í1, 2, 3, 5, 7, 8, 9ý
A Ç B = í2, 4ý A Ç B Ç C = í2ý
Representación gráfica de la unión:
 Los Los elementos comunes se colocan en la intersección de los aros u óvalos.
Los Los elementos comunes se colocan en la intersección de los aros u óvalos. Intersección de conjuntos:
Dados dos conjuntos A y B, el conjunto formado por los elementos comunes de A y B se llama intersección de A y B, es decir corresponde a los elementos que pertenecen al conjunto A y pertenecen al conjunto B
y se simboliza así: A Ç B = íx / x Î A Ù x Î Bý.
Ejemplo: Si A = í2, 3, 4, 6ý B = í0, 2, 4, 8 ý C = í1, 2, 3, 5, 7, 8, 9ý
A Ç B = í2, 4ý A Ç B Ç C = í2ý
Representación gráfica de la intersección:
Son solamente los elementos repetidos en los conjuntos dados.
Diferencia entre conjuntos:
Dados 2 conjuntos A y B, el conjunto formado por los elementos que pertenecen al conjunto A y no pertenecen al conjunto B se llama la diferencia entre A y B
y se simboliza así: A – B: A – B = íx / x Î A Ù x Ï Bý.
Ejemplo: Si A = í2, 3, 4, 6ý B = í0, 2, 4, 8 ý
A – B = í3, 6 ý B – A = í0, 8 ý
Representación gráfica de la diferencia:
Complemento de un conjunto:
Dado un conjunto universal U y un conjunto A, se define como complemento de A, al conjunto formado por todos los elementos que le faltan al conjunto A, para ser igual al conjunto U
y se simboliza así: A' = íx / x Î U Ù x Ï Aý.
Ejemplo: Si U = ílos números dígitosý A = ílos números dígitos imparesý
Hallar el complemento de A. ( A' )
Primero determinamos los conjuntos U y A por extensión:
U = í0,1,2,3,4,5,6,7,8,9ý A = í1,3,5,7,9ý A' = í0,2,4,6,8ý
Representación gráfica del complemento:
Suscribirse a:
Comentarios (Atom)